사이파이 튜토리얼#
웹 광고 한번 눌러주세요!!!
주요 모듈
6가지 대표 하위 메소드중 통계분석을 위한 stats를 위주로 학습
scipy
│
├── 01 integrate 수치적분, 미분방정식
│
├── 02 linalg (선형대수, 매트릭스 분해)
│
├── 03 optimize (방정식 해 구하는 알고리즘, 함수 최적화)
│
├── 04 signal (신호 관련)
│
├── 05 sparse (희소 행렬, 희소 선형 시스템)
│
└── 06 stats (통계 분석)
stats 하위 모듈
252개
from scipy import stats
print(len([x for x in dir(stats) if x[0] !='_' ]))
252
stats 주요 모듈#
scipy.stats
│
├── 01 T-test
│ │
│ ├── ttest_1samp (단일표본 t검정)
│ ├── ttest_ind (독립표본 t검정)
│ └── ttest_rel (대응표본 t검정)
│
├── 02 비모수 검정
│ │
│ ├── mannwhitneyu (맨-휘트니 U 검정 - 중위수 , 윌콕슨 순위합 검정과 동일하다 볼 수 있음)
│ ├── ranksums (윌콕슨 순위합 검정 - 중위수)
│ └── wilcoxon (윌콕슨 부호 순위합 검정)
│
├── 03 정규정 검정
│ │
│ ├── anderson (Anderson-Darling , 데이터수가 상대적으로 많을 때)
│ ├── kstest (Kolmogorov-Smirnov , 데이터수가 상대적으로 많을 때)
│ ├── mstats.normaltest
│ └── shapiro (shapiro, 노말분포 가장 엄격하게 검정, 데이터수가 상대적으로 적을때)
│
├── 04 등분산 검정
│ │
│ ├── bartlett
│ ├── fligner
│ └── levene
│
├── 05 카이제곱검정
│ │
│ ├── chi2_contingency (카이제곱독립검정, 독립성 검정)
│ ├── chisquare (카이제곱검정 , 적합도 검정)
│ └── fisher_exact (피셔 정확 검정 - 빈도수가 5개 이하 셀의 수가 전체 셀의 20%이상일 경우 사용 )
│
└── 06 ANOVA (일원분산분석)
│
└── f_oneway (분산 분석은 statmodels 모듈이 더 좋음! )
dir , help를 이용해서 파라미터들 찾아가며 사용하기
예제 데이터는 랜덤 생성하였습니다
정규성 검정#
Question
다음 데이터의 정규성을 검증하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/normal1.csv')
plt.hist(df)
plt.show()

Show code cell content
from scipy.stats import shapiro
print(shapiro(df))
# 샤피로 검정시 p-value가 0.34이므로 유의수준 5%에서 귀무가설("데이터는 정규성을 가진다")을 기각할 수 없다
ShapiroResult(statistic=0.9981446862220764, pvalue=0.3485966622829437)
Question
다음 데이터의 정규성을 검증하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/normal3.csv')
plt.hist(df)
plt.show()

Show code cell content
from scipy.stats import shapiro
print(shapiro(df))
# 샤피로 검정시 p-value가 2.3e-16 이므로 유의수준 5%에서 귀무가설인 "데이터는 정규성을 가진다"를 기각하고 대립가설을 채택한다
# 데이터는 정규성을 가지지 않는다
ShapiroResult(statistic=0.9578887224197388, pvalue=2.309859641255865e-16)
Question
위의 데이터를 log변환 한 후에 정규성을 가지는지 확인하라
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/normal3.csv')
log_y_data = np.log1p(df)
plt.hist(log_y_data)
plt.show()

Show code cell content
from scipy.stats import shapiro
print(shapiro(log_y_data))
# 샤피로 검정시 p-value가 0.17이므로 유의수준 5%에서 귀무가설("데이터는 정규성을 가진다")을 기각할 수 없다
ShapiroResult(statistic=0.9976893067359924, pvalue=0.17551212012767792)
Question
다음 데이터의 정규성을 검증하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/normal6.csv')
plt.hist(df)
plt.show()

Show code cell content
from scipy.stats import shapiro
print(shapiro(df))
# 샤피로 검정시 p-value가 0.15 이므로 유의수준 5%에서 귀무가설("데이터는 정규성을 가진다")을 기각할 수 없다.
# 하지만 경고 메세지에서도 보이듯이 5000개 초과의 샘플에 대해서는 샤피로 검정은 정확하지 않을 수 있다.
from scipy.stats import anderson
# anderson 검정을 실시한다
print(anderson(df['data'].values))
# anderson 검정 결과의 의미는 아래 링크에서 확인 가능
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.anderson.html
# significance_level는 유의 확률값을 나타내며 critical_values는 각 유의 확률값의 기준점이 된다.
# 5%유의 수준에서 검정을 진행하려면 statistic값인 0.82이 significance_level 이 5.에 위치한 인덱스를
# critical_values값에서 비교하면 된다. 그 값은 0.786이므로 이보다 큰 0.82을 가지므로
# 귀무가설을 기각하고 대립가설을 채택한다 -> 데이터는 정규성을 가지지 않는다고 판단한다. (p-value와 기각기준 부등호 개념이 반대)
ShapiroResult(statistic=0.9995355606079102, pvalue=0.15070641040802002)
AndersonResult(statistic=0.8266993530414766, critical_values=array([0.576, 0.656, 0.786, 0.917, 1.091]), significance_level=array([15. , 10. , 5. , 2.5, 1. ]))
/Library/Frameworks/Python.framework/Versions/3.8/lib/python3.8/site-packages/scipy/stats/morestats.py:1681: UserWarning: p-value may not be accurate for N > 5000.
warnings.warn("p-value may not be accurate for N > 5000.")
단일 표본 t검정 (one-sample)#
Question
100명의 키 정보가 들어 있는 데이터가 있다.데이터가 정규성을 만족하는지 확인하라.
그리고 평균키는 165라 판단할수 있는지 귀무가설과 대립가설을 설정한 후 유의수준 5%로 검정하라.
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/height1.csv')

Show code cell content
from scipy.stats import ttest_1samp
from scipy.stats import shapiro
from scipy.stats import wilcoxon
# 정규성 검정 샤피로
static, pvalue = shapiro(df)
print('샤피로 정규성 검정 p-value : ',pvalue,'이므로')
if pvalue < 0.05:
print('귀무가설을 기각한다. 정규성을 만족하지 않으므로 비모수 검정을 진행한다. 윌콕슨 순위 부호 검정을 진행한다.\n')
print('윌콕슨 순위 부호 검정의 귀무가설은 "100명 키의 평균은 165이다." 이며 대립가설은 "100명 키의 평균은 165가 아니다." 이다')
#윌콕슨 부호순위 검정
static, pvalue = wilcoxon(df['height']-165) # or static, pvalue = wilcoxon(df['height'], np.ones(len(df)) *165)
if pvalue < 0.05:
print(f'검정 결과 pvalue는 {pvalue}로 결과는 귀무가설을 기각하고 대립가설을 채택한다.')
else:
print(f'검정 결과 pvalue는 {pvalue}로 결과는 귀무가설을 기각하지 않는다.')
else:
print('귀무가설을 기각하지 않는다. 정규성을 만족하므로 단일표본 검정으로 확인한다.\n')
print('단일표본 t-test의 귀무가설은 "100명 키의 평균은 165이다." 이며 대립가설은 "100명 키의 평균은 165가 아니다." 이다')
#단일 표본 t 검정
static, pvalue = ttest_1samp(df['height'],165)
if pvalue < 0.05:
print(f'검정 결과 pvalue는 {pvalue}로 결과는 귀무가설을 기각하고 대립가설을 채택한다.')
else:
print(f'검정 결과 pvalue는 {pvalue}로 결과는 귀무가설을 기각하지 않는다.')
샤피로 정규성 검정 p-value : 0.455832302570343 이므로
귀무가설을 기각하지 않는다. 정규성을 만족하므로 단일표본 검정으로 확인한다.
단일표본 t-test의 귀무가설은 "100명 키의 평균은 165이다." 이며 대립가설은 "100명 키의 평균은 165가 아니다." 이다
검정 결과 pvalue는 0.0018367171548080209로 결과는 귀무가설을 기각하고 대립가설을 채택한다.
Question
100명의 키 정보가 들어 있는 데이터가 있다.데이터가 정규성을 만족하는지 확인하라.
그리고 평균키는 165라 판단할수 있는지 귀무가설과 대립가설을 설정한 후 유의수준 5%로 검정하라.
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/height2.csv')
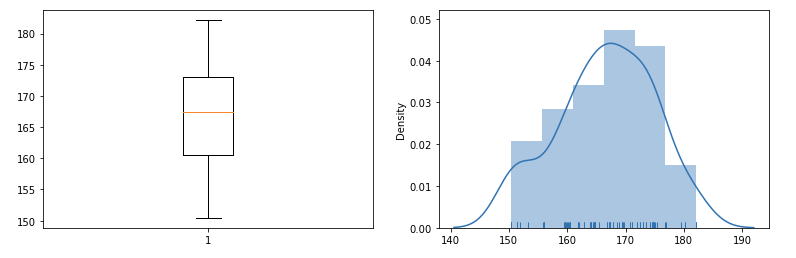
Show code cell content
from scipy.stats import ttest_1samp
from scipy.stats import shapiro
from scipy.stats import wilcoxon
# 정규성 검정 샤피로
static, pvalue = shapiro(df)
print('샤피로 정규성 검정 p-value : ',pvalue,'이므로')
if pvalue < 0.05:
print('귀무가설을 기각한다. 정규성을 만족하지 않으므로 비모수 검정을 진행한다. 윌콕슨 순위 부호 검정을 진행한다.\n')
print('윌콕슨 순위 부호 검정의 귀무가설은 "100명 키의 평균은 165이다." 이며 대립가설은 "100명 키의 평균은 165가 아니다." 이다')
#윌콕슨 부호순위 검정
static, pvalue = wilcoxon(df['height']-165) # or static, pvalue = wilcoxon(df['height'], np.ones(len(df)) *165)
if pvalue < 0.05:
print(f'검정 결과 pvalue는 {pvalue}로 결과는 귀무가설을 기각하고 대립가설을 채택한다.')
else:
print(f'검정 결과 pvalue는 {pvalue}로 결과는 귀무가설을 기각하지 않는다.')
else:
print('귀무가설을 기각하지 않는다. 정규성을 만족하므로 단일표본 검정으로 확인한다.\n')
print('단일표본 t-test의 귀무가설은 "100명 키의 평균은 165이다." 이며 대립가설은 "100명 키의 평균은 165가 아니다." 이다')
#단일 표본 t 검정
static, pvalue = ttest_1samp(df['height'],165)
if pvalue < 0.05:
print(f'검정 결과 pvalue는 {pvalue}로 결과는 귀무가설을 기각하고 대립가설을 채택한다.')
else:
print(f'검정 결과 pvalue는 {pvalue}로 결과는 귀무가설을 기각하지 않는다.')
샤피로 정규성 검정 p-value : 0.013552471995353699 이므로
귀무가설을 기각한다. 정규성을 만족하지 않으므로 비모수 검정을 진행한다. 윌콕슨 순위 부호 검정을 진행한다.
윌콕슨 순위 부호 검정의 귀무가설은 "100명 키의 평균은 165이다." 이며 대립가설은 "100명 키의 평균은 165가 아니다." 이다
검정 결과 pvalue는 0.04880534424649582로 결과는 귀무가설을 기각하고 대립가설을 채택한다.
등분산 검정#
Question
두개 학급의 시험성적에 대한 데이터이다 그룹간 등분산 검정을 시행하라
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/scipy2.csv')
df.head()
| class | score | |
|---|---|---|
| 0 | A | 84 |
| 1 | A | 59 |
| 2 | A | 49 |
| 3 | A | 57 |
| 4 | A | 82 |
Show code cell content
from scipy.stats import bartlett
from scipy.stats import fligner
from scipy.stats import levene
a = df[df['class'] =='A'].score
b = df[df['class'] =='B'].score
print(bartlett(a,b))
print(fligner(a,b,center='median')) #default
print(fligner(a,b,center='mean'))
print(levene(a,b, center='median')) #default
print(levene(a,b,center='mean'))
# 등분산검정의 방법은 3가지가 있다. pvalue값은 5% 유의수준이라면 0.05보다 작은 경우 "각 그룹은 등분산이다"라는 귀무가설을 기각한다
# 아래의 결과를 보면 모두 0.05보다 크므로 귀무가설을 기각할수 없음을 알 수 있다.
BartlettResult(statistic=0.26035880448930865, pvalue=0.609873758447687)
FlignerResult(statistic=0.7281251154135562, pvalue=0.39349158741002765)
FlignerResult(statistic=0.8272211734319945, pvalue=0.36307728836821906)
LeveneResult(statistic=0.3145466542912649, pvalue=0.5751662820554713)
LeveneResult(statistic=0.5086970687685527, pvalue=0.4760514837800255)
Question
두개 학급의 시험성적에 대한 데이터이다 그룹간 등분산 검정을 시행하라
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/scipy3.csv')
df.head()
| class | score | |
|---|---|---|
| 0 | A | 32 |
| 1 | A | 69 |
| 2 | A | 68 |
| 3 | A | 60 |
| 4 | A | 78 |
Show code cell content
from scipy.stats import bartlett
from scipy.stats import fligner
from scipy.stats import levene
a = df[df['class'] =='A'].score
b = df[df['class'] =='B'].score
print(bartlett(a,b))
print()
print(fligner(a,b,center='median')) #default
print(fligner(a,b,center='mean'))
print(levene(a,b, center='median')) #default
print(levene(a,b,center='mean'))
# bartlett 검정 결과 pvalue는 0.05보다 크고
# fligner, levene 검정 결과 pvalue는 0.05보다 작다.
# fligner, levene는 bartlett보다 좀더 robust하다는 특징이 있다.
# 어떤 검정의 결과를 사용해야하는지는 정해지지 않았지만 상황에 따라 특징들을 서술할 수 있다면 문제 없지 않을까...
BartlettResult(statistic=1.5116783794562305, pvalue=0.2188831590902503)
FlignerResult(statistic=4.960366756026232, pvalue=0.025934706256615564)
FlignerResult(statistic=4.94724457924667, pvalue=0.026132286002684912)
LeveneResult(statistic=4.307122424591436, pvalue=0.03848734007752694)
LeveneResult(statistic=4.342327020297874, pvalue=0.0377066528874248)
Question
두개 학급의 시험성적에 대한 데이터이다 그룹간 등분산 검정을 시행하라
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/scipy6.csv')
df.head()
| A | B | |
|---|---|---|
| 0 | 44 | 36 |
| 1 | 61 | 92 |
| 2 | 76 | 41 |
| 3 | 64 | 45 |
| 4 | 65 | 35 |
Show code cell content
from scipy.stats import bartlett
from scipy.stats import fligner
from scipy.stats import levene
print(bartlett(df.A,df.B))
print(fligner(df.A,df.B))
print(levene(df.A,df.B))
# BartlettResult -> 등분산이다 // FlignerResult , LeveneResult -> 등분산이 아니다
BartlettResult(statistic=2.3832178811043527, pvalue=0.12264468401745829)
FlignerResult(statistic=5.124831619122788, pvalue=0.023585858890699054)
LeveneResult(statistic=5.147914610463281, pvalue=0.023868975493455683)
Question
두개 학급의 시험성적에 대한 데이터이다 그룹간 등분산 검정을 시행하라
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/scipy5.csv')
df.head()
| A | B | |
|---|---|---|
| 0 | 74 | 30.0 |
| 1 | 30 | 59.0 |
| 2 | 35 | 69.0 |
| 3 | 45 | 88.0 |
| 4 | 74 | 68.0 |
Show code cell content
from scipy.stats import bartlett
from scipy.stats import fligner
from scipy.stats import levene
print(bartlett(df.A,df.B))
print(bartlett(df.A,df.B.dropna()))
print()
print(fligner(df.A,df.B))
print(fligner(df.A,df.B.dropna()))
print()
print(levene(df.A,df.B))
print(levene(df.A,df.B.dropna()))
# bartlett ,fligner 두 검정은 nan값을 지우고 사용해야한다. LeveneResult의 경우 nan값이 포함된다면 연산이 제대로 안된다
BartlettResult(statistic=4.119254834772108, pvalue=0.04239774936707851)
BartlettResult(statistic=3.024072692680794, pvalue=0.08203720607748438)
FlignerResult(statistic=372.546422798273, pvalue=5.22112391778621e-83)
FlignerResult(statistic=7.710320541528441, pvalue=0.005490600130793619)
LeveneResult(statistic=nan, pvalue=nan)
LeveneResult(statistic=8.008595918808284, pvalue=0.004851565077063284)
독립표본 검정 (Independent)#
독립 표본 t검정의 경우 집단의 정규성에 따라 접근방식이 다르다
정규성 검정은 shapiro , anderson(샘플 5000개 이상) 을 통해 확인
데이터가 정규성을 가지는 경우(모수적 검정)
두 집단의 등분산 검정을 한 후
from scipy.stats import ttest_ind
등분산일 경우
\(
\begin{align}
t = \dfrac{\bar{x}_1 - \bar{x}_2}{s \cdot \sqrt{\dfrac{1}{N_1}+\dfrac{1}{N_2}}}
\tag{equal_var=True}
\end{align}
\)
등분산이 아닐 경우
\(
\begin{align}
t = \dfrac{\bar{x}_1 - \bar{x}_2}{\sqrt{\dfrac{s_1^2}{N_1} + \dfrac{s_2^2}{N_2}}}
\tag{equal_var=False , welch t-test}
\end{align}
\)
데이터가 정규성을 가지지 않는 경우(비모수적 검정)
Question
두개 학급의 시험성적에 대한 데이터이다. 두 학습의 시험 평균(비모수검정의 경우 중위값)은 동일하다 말할 수 있는지 확인 하라
import pandas as pd
import matplotlib.pyplot as plt
df1 = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/ind1.csv')
df2 = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/ind2.csv')
plt.hist(df1,label='df1',alpha=0.4)
plt.hist(df2,label="df2",alpha=0.4)
plt.xlabel('Score bins')
plt.ylabel('Counts')
plt.legend()
plt.show()

Show code cell content
from scipy.stats import shapiro
print(shapiro(df1))
print(shapiro(df2))
# 두 그룹 모두 Shapiro검정 결과 귀무가설(정규성을 가진다)을 기각 하지 못한다. 두 그룹은 정규성을 가진다.
from scipy.stats import levene
print()
print(levene(df1['data'],df2['data']))
# 두그룹은 levene 검정을 확인해 본결과 pvalue 는 0.11로 귀무가실을 기각히지 못한다. 그러므로 등분산은 가진다
from scipy.stats import ttest_ind
print()
print(ttest_ind(df1,df2,equal_var=True))
# 등분산이기 때문에 equal_var=True 파라미터를 주고 ttest_ind 모듈을 이용하여 t test를 진행한다
# pvalue는 0.006이므로 귀무가설(각 그룹의 평균값은 동일하다)를 기각하고 대립가설을 채택한다
Question
두개 학급의 시험성적에 대한 데이터이다. 두 학습의 시험 평균(비모수검정의 경우 중위값)은 동일하다 말할 수 있는지 확인 하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/scipy5.csv')
plt.hist(df['A'],alpha=0.5,label='A')
plt.hist(df['B'].dropna(),alpha=0.5,label="B")
plt.xlabel('Score bins')
plt.ylabel('Counts')
plt.legend()
plt.show()

Show code cell content
# 데이터 분포를 확인해보니 정규성을 위해하는 것 처럼 보인다.
# 두그룹중 한 그룹만 정규성을 위배해도 독립표본 t-검정을 할 수 없다
print(shapiro(df['B'].dropna()))
print(shapiro(df['A']))
# 두 그룹 모두 Shapiro검정 결과 귀무가설(정규성을 가진다)을 기각한다. 정규성을 위배한다. 그러므로 비모수 검정을 실시해야한다.
from scipy.stats import mannwhitneyu , ranksums
print()
print(mannwhitneyu(df['A'],df['B'].dropna()))
print(ranksums(df['A'],df['B'].dropna()))
# Mann-Whitney U Test 검정 결과 pvalue는 0.49값으로 귀무가설(평균은같다)를 기각 할 수 없다. 두그룹의 평균은 동일하다 말할 수 있다.
# 윌콕슨 순위합 검정(ranksums)으로 확인 해봐도 같은 결과가 나온다.
ShapiroResult(statistic=0.9639444351196289, pvalue=0.00013572089665103704)
ShapiroResult(statistic=0.93753981590271, pvalue=6.175894240456614e-10)
MannwhitneyuResult(statistic=26964.0, pvalue=0.4903729188075009)
RanksumsResult(statistic=0.02446942170858557, pvalue=0.9804781743503561)
Question
두개 그룹에 대한 수치형 데이터이다. 두 그룹의 평균은 동일하다 말할 수 있는지 검정하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/ind3.csv')
plt.hist(df[df['group'] =='a'].data,label='A',alpha=0.5)
plt.hist(df[df['group'] =='b'].data,label="B",alpha=0.5)
plt.xlabel('Score bins')
plt.ylabel('Counts')
plt.legend()
plt.show()

Show code cell content
a = df[df['group'] =='a'].data
b = df[df['group'] =='b'].data
from scipy.stats import shapiro
print(shapiro(a))
print(shapiro(b))
print("두 그룹 모두 Shapiro검정 결과 귀무가설(정규성을 가진다)을 기각 하지 못한다. 두 그룹은 정규성을 가진다.")
from scipy.stats import levene
print()
print(levene(a,b))
print("두그룹은 levene 검정을 확인해 본결과 pvalue 는 0.013로 귀무가실을 기각하고 대립가설을 채택한다. 두 그룹은 등분산이 아니다")
from scipy.stats import ttest_ind
print()
print(ttest_ind(a,b,equal_var=False))
print('''등분산이 아니기 때문에 equal_var=False 파라미터를 주고 ttest_ind 모듈을 이용하여 t test를 진행한다
pvalue는 0.02이므로 귀무가설(각 그룹의 평균값은 동일하다)를 기각하고 대립가설을 채택한다
결론적으로 두 그룹은 모두 정규성을 가지지만 등분산은 아니며 평균은 동일하다고 보기 어렵다
''')
ShapiroResult(statistic=0.9834123253822327, pvalue=0.1473984718322754)
ShapiroResult(statistic=0.9831849336624146, pvalue=0.47018250823020935)
두 그룹 모두 Shapiro검정 결과 귀무가설(정규성을 가진다)을 기각 하지 못한다. 두 그룹은 정규성을 가진다.
LeveneResult(statistic=6.185601018015722, pvalue=0.013750484571911342)
두그룹은 levene 검정을 확인해 본결과 pvalue 는 0.013로 귀무가실을 기각하고 대립가설을 채택한다. 두 그룹은 등분산이 아니다
Ttest_indResult(statistic=-2.1949470315829265, pvalue=0.029512802991767915)
등분산이 아니기 때문에 equal_var=False 파라미터를 주고 ttest_ind 모듈을 이용하여 t test를 진행한다
pvalue는 0.02이므로 귀무가설(각 그룹의 평균값은 동일하다)를 기각하고 대립가설을 채택한다
결론적으로 두 그룹은 모두 정규성을 가지지만 등분산은 아니며 평균은 동일하다고 보기 어렵다
Question
두개 그룹에 대한 수치형 데이터이다. 두 그룹의 평균은 동일하다 말할 수 있는지 검정하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/ind6.csv')
plt.hist(df['a'],alpha=0.5,label='A')
plt.hist(df['b'],alpha=0.5,label="B")
plt.xlabel('Score bins')
plt.ylabel('Counts')
plt.legend()
plt.show()

Show code cell content
a = df['a'].dropna()
b = df['b'].dropna()
from scipy.stats import shapiro
print(shapiro(a))
print(shapiro(b))
print("두 그룹 모두 Shapiro검정 결과 귀무가설(정규성을 가진다)을 기각 하지 못한다. 두 그룹은 정규성을 가진다.")
from scipy.stats import levene
print()
print(levene(a,b))
print("두그룹은 levene 검정을 확인해 본결과 pvalue 는 0.047로 귀무가실을 기각하고 대립가설을 채택한다. 두 그룹은 등분산이 아니다")
from scipy.stats import ttest_ind
print()
print(ttest_ind(a,b,equal_var=False))
print('''등분산이 아니기 때문에 equal_var=False 파라미터를 주고 ttest_ind 모듈을 이용하여 t test를 진행한다
pvalue는 0.99이므로 귀무가설(각 그룹의 평균값은 동일하다)를 기각하기 어렵다
결론적으로 두 그룹은 모두 정규성을 가지지만 등분산은 아니며 평균은 동일하다고 볼 수 있다
''')
ShapiroResult(statistic=0.9865895509719849, pvalue=0.28390026092529297)
ShapiroResult(statistic=0.9854329228401184, pvalue=0.5937777757644653)
두 그룹 모두 Shapiro검정 결과 귀무가설(정규성을 가진다)을 기각 하지 못한다. 두 그룹은 정규성을 가진다.
LeveneResult(statistic=3.9862856894158347, pvalue=0.04731495612868527)
두그룹은 levene 검정을 확인해 본결과 pvalue 는 0.047로 귀무가실을 기각하고 대립가설을 채택한다. 두 그룹은 등분산이 아니다
Ttest_indResult(statistic=0.0015963310698567188, pvalue=0.9987289046092704)
등분산이 아니기 때문에 equal_var=False 파라미터를 주고 ttest_ind 모듈을 이용하여 t test를 진행한다
pvalue는 0.99이므로 귀무가설(각 그룹의 평균값은 동일하다)를 기각하기 어렵다
결론적으로 두 그룹은 모두 정규성을 가지지만 등분산은 아니며 평균은 동일하다고 볼 수 있다
대응표본 t 검정 (paired)#
Question
특정 질병 집단의 투약 전후의 혈류량 변화를 나타낸 데이터이다. 투약 전후의 변화가 있는지 검정하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/rel2.csv')
fig ,ax = plt.subplots(1,2)
ax[0].boxplot(df['before'])
ax[1].boxplot(df['after'])
ax[0].set_xticklabels(['before'])
ax[1].set_xticklabels(['after'])
ax[0].set_ylim(100,350)
ax[1].set_ylim(100,350)
ax[1].get_yaxis().set_visible(False)
ax[0].set_ylabel('value')
plt.show()

Show code cell content
from scipy.stats import shapiro
before = df['before']
after = df['after']
print(shapiro(before))
print(shapiro(after))
from scipy.stats import levene
print()
print(levene(before,after))
from scipy.stats import ttest_rel
print(ttest_rel(before,after))
# 정규성 가짐 , 등분산성 가짐 -> 대응표본의 경우 등분산성이 파라미터에 영향을 주지않음,
# 대응표본 t 검정 결과 pvalue는 0.01로 유의수준 5%내에서 귀무가설을 기각한다 (전 후 평균은 같지 않다)
ShapiroResult(statistic=0.9907894134521484, pvalue=0.6065712571144104)
ShapiroResult(statistic=0.9916958808898926, pvalue=0.6923439502716064)
LeveneResult(statistic=0.06427968690211128, pvalue=0.8000741651677987)
Ttest_relResult(statistic=-2.5535473487670677, pvalue=0.011926744724546513)
Question
특정 질병 집단의 투약 전후의 혈류량 변화를 나타낸 데이터이다. 투약 전후의 변화가 있는지 검정하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/rel3.csv')
fig ,ax = plt.subplots(1,2)
ax[0].boxplot(df['before'])
ax[1].boxplot(df['after'])
ax[0].set_xticklabels(['before'])
ax[1].set_xticklabels(['after'])
ax[0].set_ylim(130,300)
ax[1].set_ylim(130,300)
ax[1].get_yaxis().set_visible(False)
ax[0].set_ylabel('value')
plt.show()

Show code cell content
from scipy.stats import shapiro
before = df['before']
after = df['after']
print(shapiro(before))
print(shapiro(after))
from scipy.stats import levene
print()
print(levene(before,after))
from scipy.stats import ttest_rel
print(ttest_rel(before,after))
print()
# 정규성 가짐 , 등분산성 가짐 -> 대응표본의 경우 등분산성이 파라미터에 영향을 주지않음,
# 대응표본 t 검정 결과 pvalue는 0.85로 유의수준 5%내에서 귀무가설을 기각할 수 없다 (전 후 평균은 같다)
ShapiroResult(statistic=0.9920635223388672, pvalue=0.7270597219467163)
ShapiroResult(statistic=0.992019534111023, pvalue=0.7229286432266235)
LeveneResult(statistic=1.3463330638203617, pvalue=0.24708279045237214)
Ttest_relResult(statistic=0.188900575991026, pvalue=0.8504925317234707)
Question
특정 집단의 학습 전후 시험 성적 변화를 나타낸 데이터이다. 시험 전과 후에 차이가 있는지 검정하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/rel1.csv')
fig ,ax = plt.subplots(1,2)
ax[0].boxplot(df['before'])
ax[1].boxplot(df['after'])
ax[0].set_xticklabels(['before'])
ax[1].set_xticklabels(['after'])
ax[0].set_ylim(145,170)
ax[1].set_ylim(145,170)
ax[1].get_yaxis().set_visible(False)
ax[0].set_ylabel('value')
plt.show()

Show code cell content
from scipy.stats import shapiro
before = df['before']
after = df['after']
print(shapiro(before))
print(shapiro(after))
from scipy.stats import levene
print()
print(levene(before,after))
from scipy.stats import ttest_rel
print(ttest_rel(before,after))
print()
from scipy.stats import wilcoxon
print(wilcoxon(before,after))
# 정규성을 가지지 않음 , 등분산성 가짐 -> 대응표본의 경우 등분산성이 파라미터에 영향을 주지않음,
# 정규성을 가지지 않으므로 대응 표본 검정중 비모수 검정인 윌콕슨 부호순위 검정을 진행해야한다 (scipy.stats.wilcoxon)
# t-test의 경우 전후 변화에 대한 귀무가설을 기각되지만 윌콕슨 부호순위 검정을 통해서 확인해봤을때 귀무가설을 기각할 수 없다
ShapiroResult(statistic=0.9173726439476013, pvalue=0.001897332607768476)
ShapiroResult(statistic=0.9448971152305603, pvalue=0.021141061559319496)
LeveneResult(statistic=0.14329522146179022, pvalue=0.7058456563194881)
Ttest_relResult(statistic=-2.187138399865287, pvalue=0.03353471744538162)
WilcoxonResult(statistic=437.0, pvalue=0.12098409484052809)
Question
한 기계 부품의 rpm 수치를 두가지 다른 상황에서 측정했다.(총 70세트) b 상황이 a 상황보다 rpm값이 높다고 말할 수 있는지 검정하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/rel4.csv')
fig ,ax = plt.subplots(1,2)
ax[0].boxplot(df[df['group']=='a'].rpm)
ax[1].boxplot(df[df['group']=='b'].rpm)
ax[0].set_xticklabels(['a'])
ax[1].set_xticklabels(['b'])
ax[0].set_ylim(430,600)
ax[1].set_ylim(430,600)
ax[1].get_yaxis().set_visible(False)
ax[0].set_ylabel('rpm')
plt.show()

Show code cell content
from scipy.stats import shapiro
a = df[df['group']=='a'].rpm
b = df[df['group']=='b'].rpm
print(shapiro(a))
print(shapiro(b))
from scipy.stats import levene
print()
print(levene(a,b))
from scipy.stats import ttest_rel
print(ttest_rel(a,b,alternative='greater'))
print()
# 정규성을 가짐 , 등분산성 가짐 -> 대응표본의 경우 등분산성이 파라미터에 영향을 주지않음,
# a,b,alternative='greater' 의 의미는 a >b가 대립가설이 된다는 것이다. p-value는 0.96으로
# 귀무가설인 a<=b를 기각하지 못한다. 그러므로 b상황이 a 상황보다 rpm 값이 크다고 이야기 할수 있다.
ShapiroResult(statistic=0.9907213449478149, pvalue=0.8884111046791077)
ShapiroResult(statistic=0.984674870967865, pvalue=0.5505106449127197)
LeveneResult(statistic=0.06716114122680159, pvalue=0.7959020864923277)
Ttest_relResult(statistic=-1.9018108294460812, pvalue=0.9693143365355352)
카이제곱 검정 (교차분석)#
일원 카이제곱검정 (chisquare , 카이제곱 적합도 검정)
한 개의 요인에 의해 k개의 범주를 가질때 이론적 분포를 따르는지 검정
이원 카이제곱검정 (chi2_contingency ,fisher_exact(빈도수 5개 이하 셀이 20% 이상일때) , 카이제곱독립검정)
모집단이 두개의 변수에 의해 범주화 되었을 때, 두 변수들 사이의 관계가 독립인지 아닌지 검정
Question
144회 주사위를 던졌을때, 각 눈금별로 나온 횟수를 나타낸다. 이 데이터는 주사위의 분포에서 나올 가능성이 있는지 검정하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/dice.csv')
plt.bar(df.dice_number,df.counts)
plt.xlabel('dice value')
plt.ylabel('counts')
plt.show()

Show code cell content
# 주사위 눈금의 발생확률은 1/6으로 모두 동일하다. 그러므로 각 눈금의 기댓값은 실제 발생한 모든값을 6으로 나눈 값이다.
from scipy.stats import chisquare
df['expected'] = (df['counts'].sum()/6).astype('int')
print(chisquare(df.counts,df.expected))
# p-value는 0.8로 귀무가설인 "각 주사위 눈금 발생비율은 동일함"을 기각 할 수 없다
Power_divergenceResult(statistic=2.333333333333333, pvalue=0.8013589222076911)
Question
다음 데이터는 어떤 집단의 왼손잡이, 오른손 잡이의 숫자를 나타낸다. 인간의 왼손잡이와 오른손잡이의 비율을 0.2:0.8로 알려져있다.
이 집단에서 왼손과 오른손 잡이의 비율이 적합한지 검정하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/hands2.csv')
df.head()
| hands | |
|---|---|
| 0 | right |
| 1 | right |
| 2 | left |
| 3 | right |
| 4 | right |
Show code cell content
# 데이터에서
target = df.hands.value_counts().to_frame()
target['expected'] = [int(target.hands.sum()*0.8),int(target.hands.sum()*0.2)]
display(target)
from scipy.stats import chisquare
print(chisquare(target.hands,target.expected))
# 알려진 비율로 계산된 기댓값을 구하여 카이제곱검정을 시행한다.
# p-value는 0.02로 유의수준 5%이내에서 귀무가설을 기각하고 대립가설을 채택한다
# 즉 주어진 집단의 왼손, 오른손 비율은 0.2, 0.8으로 볼 수 없다
| hands | expected | |
|---|---|---|
| right | 420 | 400 |
| left | 80 | 100 |
Power_divergenceResult(statistic=5.0, pvalue=0.025347318677468325)
Question
다음 데이터는 국민 기초체력을 조사한 데이터이다. 성별과 등급이 독립적인지 검정하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/body/body.csv')
df.head()
| 측정나이 | 측정회원성별 | 신장 : cm | 체중 : kg | 체지방율 : % | 이완기혈압(최저) : mmHg | 수축기혈압(최고) : mmHg | 악력D : kg | 앉아윗몸앞으로굽히기 : cm | 교차윗몸일으키기 : 회 | 제자리 멀리뛰기 : cm | 등급 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 59.0 | M | 175.0 | 70.6 | 19.2 | 91.0 | 150.0 | 40.6 | 12.2 | 30.0 | 179.0 | C |
| 1 | 40.0 | F | 161.4 | 45.8 | 21.7 | 62.0 | 119.0 | 22.1 | 16.0 | 32.0 | 165.0 | B |
| 2 | 27.0 | M | 176.6 | 84.8 | 19.2 | 87.0 | 153.0 | 45.9 | 13.2 | 61.0 | 216.0 | B |
| 3 | 38.0 | M | 167.6 | 76.7 | 24.7 | 63.0 | 132.0 | 43.6 | 16.0 | 45.0 | 231.0 | A |
| 4 | 21.0 | M | 165.2 | 66.2 | 21.5 | 83.0 | 106.0 | 33.5 | 10.6 | 46.0 | 198.0 | C |
Show code cell content
cdf = pd.crosstab(df['측정회원성별'],df['등급'])
display(cdf)
from scipy.stats import chi2_contingency
print(chi2_contingency(cdf))
chi2 , p ,dof, expected = chi2_contingency(cdf)
print(p)
# p-value는 0에 근접하므로 측정회원성별 - 등급은 연관이 없다는 귀무가설을 기각하고, 성별관 체력 등급간에는 관련이 있다고 볼 수 있다.
| 등급 | A | B | C | D |
|---|---|---|---|---|
| 측정회원성별 | ||||
| F | 1484 | 1130 | 1147 | 1120 |
| M | 1865 | 2219 | 2202 | 2229 |
(120.06233631119409, 7.481892813401677e-26, 3, array([[1220.25, 1220.25, 1220.25, 1220.25],
[2128.75, 2128.75, 2128.75, 2128.75]]))
7.481892813401677e-26
Question
성별에 따른 동아리 활동 참석 비율을 나타낸 데이터이다. 성별과 참석간에 관련이 있는지 검정하라
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/fe2.csv',index_col=0)
df
| 불참 | 참석 | 총합 | |
|---|---|---|---|
| 남성 | 4 | 2 | 6 |
| 여성 | 1 | 9 | 10 |
| 총합 | 5 | 11 | 16 |
Show code cell content
cdf = df.iloc[:-1,:-1]
display(cdf)
from scipy.stats import chi2_contingency,fisher_exact
print(chi2_contingency(cdf))
chi2 , p ,dof, expected = chi2_contingency(cdf)
print(p)
# 카이 제곱 검정시 p-value는 0.07로 귀무가설을 기각하지 못한다. 성별과 참석여부는 관련이 없다(독립이다).
# 하지만 5보다 작은 셀이 20%가 넘어가므로(75%) 피셔의 정확검정을 사용 해야한다.
# 피셔의 정확검정시 0.03의 값을 가지므로 귀무가설을 기각한다. 성별과 참석여부는 관련이 있다. (독립이 아니다))
print(fisher_exact(cdf))
| 불참 | 참석 | |
|---|---|---|
| 남성 | 4 | 2 |
| 여성 | 1 | 9 |
(3.277575757575758, 0.07023259819117404, 1, array([[1.875, 4.125],
[3.125, 6.875]]))
0.07023259819117404
(18.0, 0.035714285714285726)

